Tutorials in Molecular Reaction Dynamics

     The following solutions are fully worked through in a PDF that is available to print.

 

    

     2.  (a) Use the equation for the total energy available to the products:

                         

             

•                

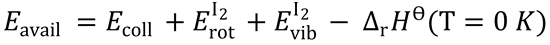
                         Δ_rH^θ = -170 kJ mol^​-1

•                ​

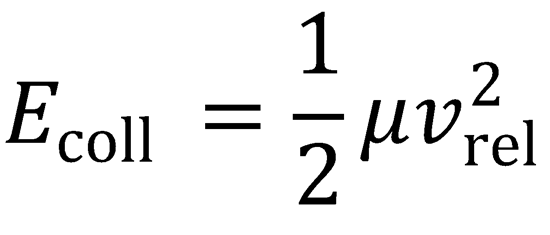
                         E_coll = 10.8 kJ mol^​-1

•                E_rot(I_​2​) = RT (using the Equipartion principle for a linear molecule: each quadratic term in the

                                             Hamiltonian contributes ½RT ​to the internal energy).

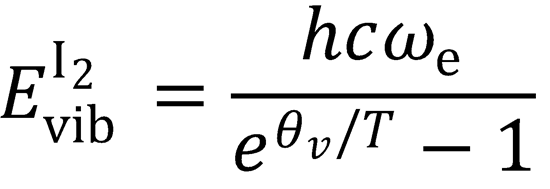•                 (the high temperature limit cannot be used here because only the lower vibrational

                                             levels are populated).

                         E_vib(I₂) = 1.426 kJ mol^-1

               

                             ∴ E_avail = 10.8 + ​RT​ + 1.426 + 170 = 184.7 kJ mol^​-1

 

         (b) |ℓ_max| = μv_relb_{max                            (1)}

 

                                                           

               

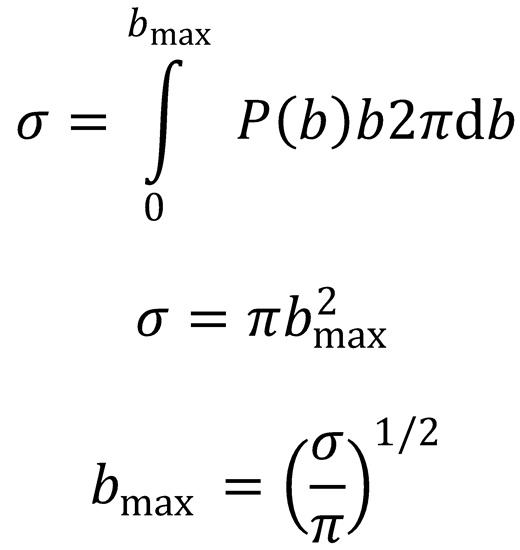
             Substitute the expression for b_max into (1) to obtain a value for |ℓ_max|:

                                                       

  

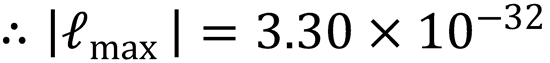
             Using the fact that :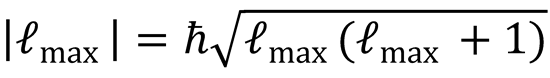

                                                           

 

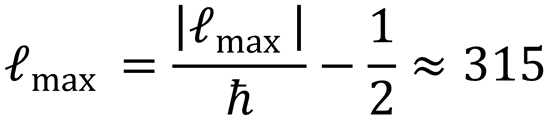
         (c) j'​ = ℓ_max ≈ 315

                                      

 

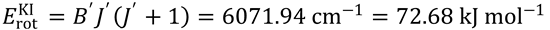
    3.  (a) Plot a graph to show consistency with the line-of-centres model:

                                                     

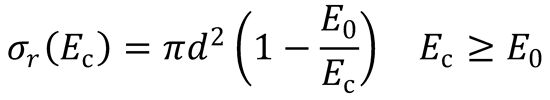
              Rearranging the equation gives:

                                                       

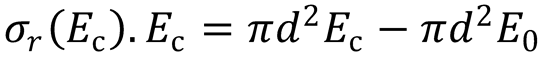
              Therefore, plot a graph of σ_r(E_c).E_c vs E_c to produce a straight line;

                      gradient = 𝜋d²

                            y-intercept = – 𝜋d²E_​0

 

Ec/kJ mol​-1	σr(Ec)/10-10 m2	σr(Ec).Ec/10-10 m​2​ kJ mol​-1
9	0.5	4.5
15	1.25	18.75
30	2.0	60
50	2.2	110

                                            

 

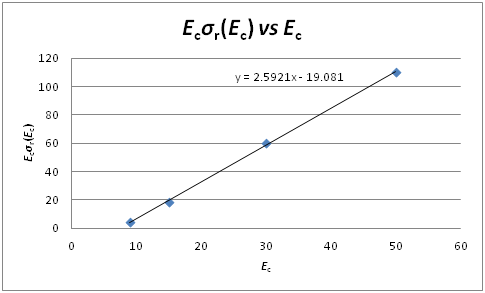
              gradient = 𝜋d² = 2.5921

              ∴ 𝜋d² = 2.59 Å²

              y-intercept = – 𝜋d²E_​0 = – 19.081

              ∴ E_​0​ = 7.36 kJ mol^-1

 

         (b) 

                                                     

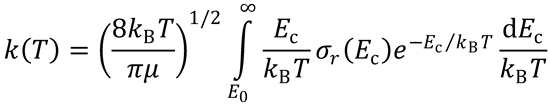
                Let ​x =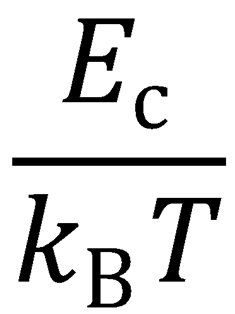 

                

                                           

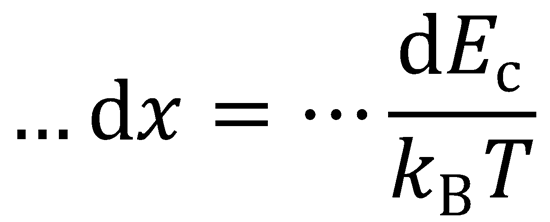
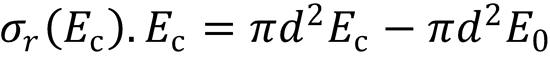
                 E_c = ​xk_BT

                                       

                                              

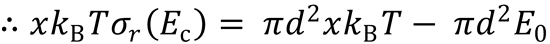
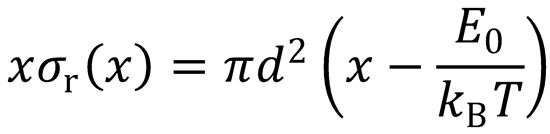
                ​E_​0​ → E_​0​/k_B​T, ​so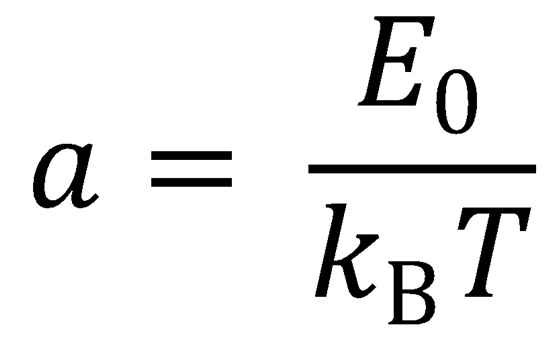                   

                                        

                                           

                                           

 

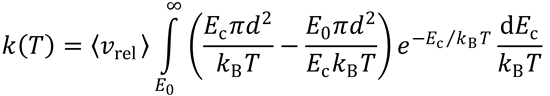
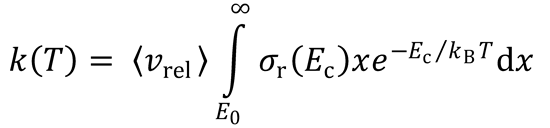
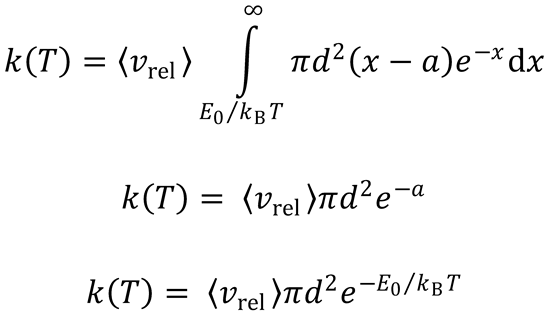
                This is identical to the expression obtained for simple collision theory (SCT).

 

  

       

       Return to Problem Set