Tutorials in Molecular Reaction Dynamics

     The following solutions are fully worked through in a PDF that is available to print.    

 

     1.  Kinematics: 

                                         

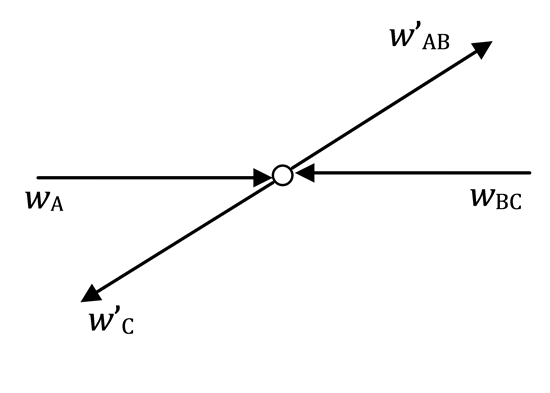
          Linear momentum conservation:

                                                        

                                               

                                           

                                             

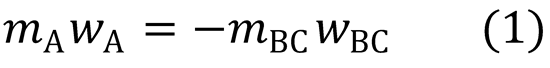
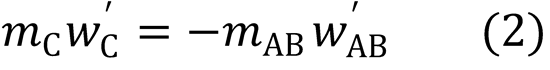
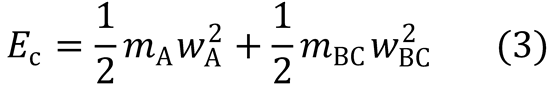
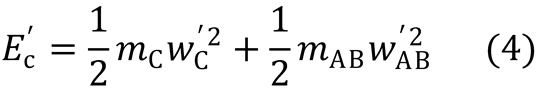
           From (1):

                                              

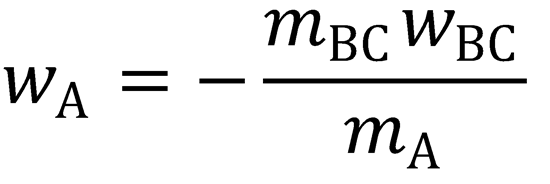
           Substitute into (3): 

                                             

                                             

                                             

 

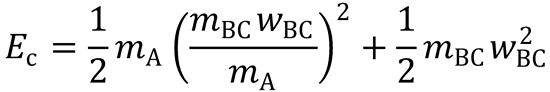
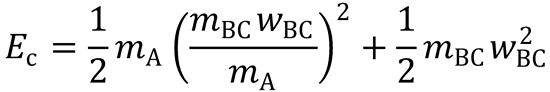
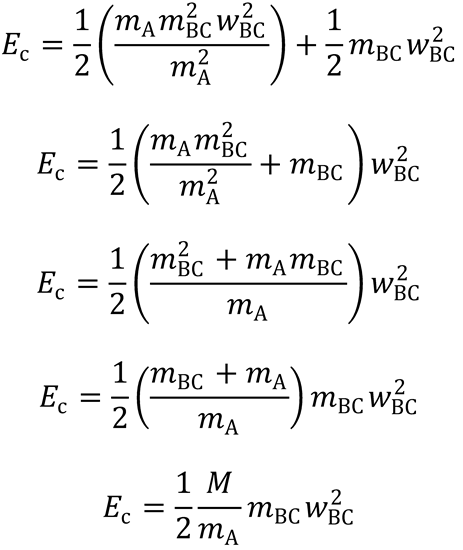
            where M = ​m_A​ + m_BC

               Similarly, from equations (2) and (4), it can be shown that:

                                                      

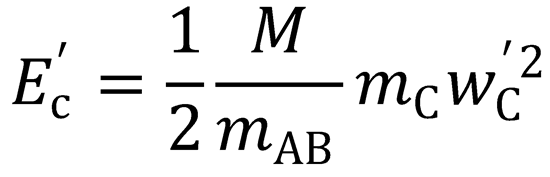
             Now, to derive Eq. (7.24):

                                                     

                                              

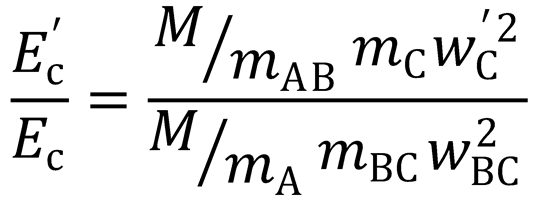
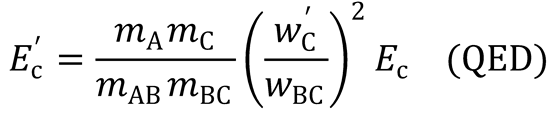
             If the C atom acts as a spectator such that ​w'_C = w_BC:

                                                       

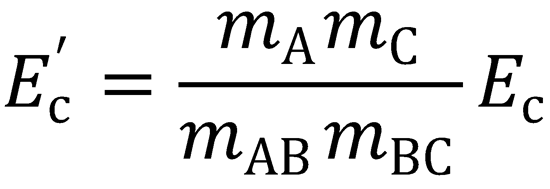
             i.e. ​E'_C = E_C when cos^​2β = ​1. This occurs when β = ​0°.

             β → ​0°, and so cos^​2​β → ​1 in a light atom transfer reaction, since m_A ≈ m_B and m_C ≈ ​m_BC​.

             Therefore, most of the available energy in this reaction is channelled into vibrational exctiation. 

             i.e. ​exothermicity is released into internal modes of motion.

 

             In a light atom departing, or attacking, reaction cos²β → 0 since m_A «  m_B. This means that β → ​90°,

             and most of the available energy goes into product translational energy. 

 

 

             Return to Problem Set