1. Starting from Eq. (4.1), derive Eq. (4.5). Make use of the expansion of the total wavefunction in nuclear (ψ)
and electronic (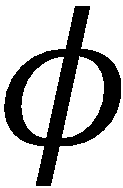
) parts:
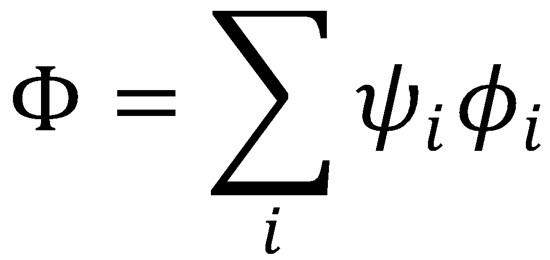
where explicit dependence on the coordinates R and r and on time has been dropped to simplify the notation.
You will need to employ Eqs. (4.2), (4.3), and (4.6). Hint: the derivation starts by substituting the above
expansion into Eq. (4.2), multiplication through by 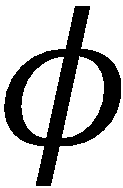j* and integration over electronic coordinates, making use
of orthonormality of the electronic wavefunctions.
2. Starting from Eq. (4.6) and using the definition in Eq. (4.7) of the kinetic energy operator,
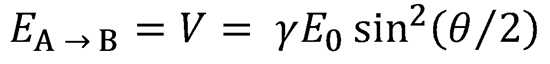
derive Eqs. (4.8) and (4.9) using the definitions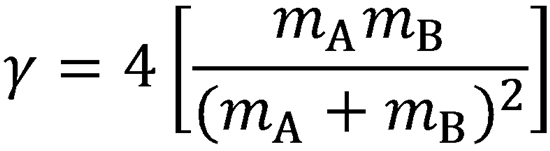 
and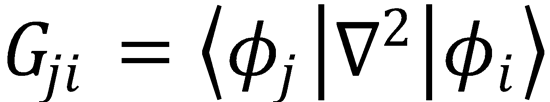 
. Hints: to obtain Eq. (4.8),
use the relationship for differentiation of the product of wavefunctions ψi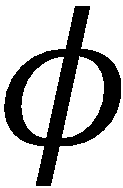i that
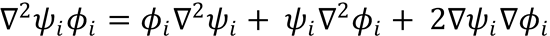, the derivation of the second equality in Eq. (4.9) requires application
of the gradient operator ∇ to both sides of the electronic Schrödinger Eq. (4.3).
3. The reaction Cs + Br2 → CsBr + Br occurs via a harpoon mechanism in which an electron transfters from Cs
to Br2 at a distance Rc at which the covalent PES for the reaction is crossed by the ionic PES for Cs+ + Br2-
ions. At large separations of the Cs and Br2, the two PESs are separated by an energy corresponding to the
difference between the ionization energy of the Cs atom (I(Cs) = 3.89 eV) and the electron affinity of the Br2,
(EA(Br2) = 2.55 eV). Estimate a value for Rc assuming that the interaction energy between Cs and Br2 on the
covalent PES varies only very weakly with separation at long range. Hence estimate the cross section for this
reaction.
4. Two diabatic states, characterized by wavefunctions ψ1 and ψ2, arise as eigenfunctions of some simple
approximate Hamiltonian for a diatomic molecule, and have energies ε1 and ε2, respectively. When the full
Hamiltonian is considered, a small interaction
between these states occurs. By considering trial wavefunctions of the form
and using the variational principle, find general expressions for the two lowest energy levels (see Study Box
4.1).
5. In the previous question, the energies ε1 and ε2 vary with internuclear separation R as ε1 = K(R—4),
ε2 = -K(R—4), whereas Δ = K/10 is a constant. Evaluate and plot the two lowest energy levels at
R = 4.0, 4.0±0.1, 4.0±0.2, 4.0±0.5, and 4.0±1.0. Plot also the ratio |c1/c2| as a function of R for each
associated eigenfunction. Comment on the results you obtain.
6. Use the Landau-Zener model (Eq. (4.11)) with the following parameters to calculate the transition
probabilities from the B3P(0+) to the Y3S-(0+) state of IBr at selected excitation photon energies in the
range shown in Figure 4.4.
|
Parameters for the IBr B and Y states |
|
|
|
Energy at crossing (cm-1) |
V12(cm-1) |
∂(V2—V1)/∂R (cm-1) Å-1 |
|
16980 |
120 |
6424 |
7. For collinear approach of an F(2P) atom to an H2 molecule, what are the allowed values of the W quantum
number (for the projection of the total angular momentum on the internuclear axis)? What values of W arise
for HF(X1S+) + H and HF(a3P) + H products? Using adiabatic correlation of W from reagents through to
products, construct a correlation diagram for the adiabatic PESs for collinear reaction of F(2P) + H2 → HF + H
and compare your result to figure 4.11.
Repeat the analysis for the reaction F + D2O → DF + OD (with the approximation of a collinear reaction).
Above Problems are available as a PDF to print
Solutions to Chapter 4 Problems