1. For a Hamiltonian of the form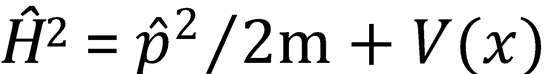 
calculate the quantities
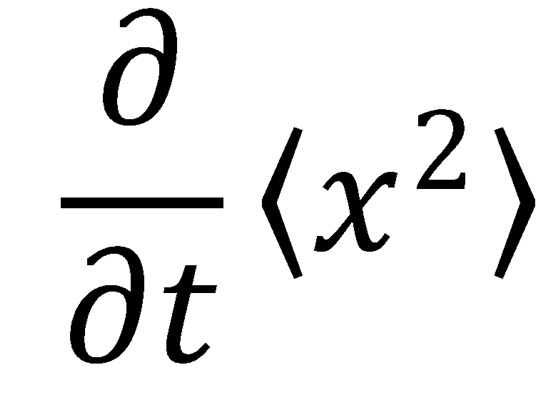and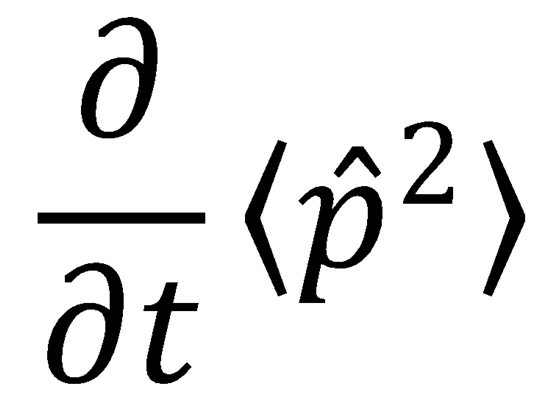 
.
Note that the commutator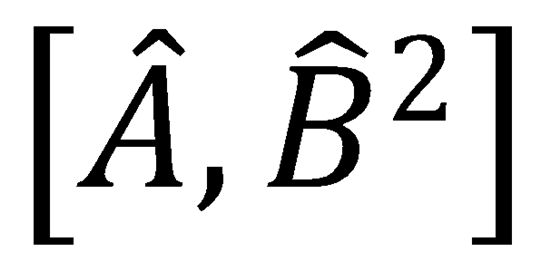 
can be written as 
.
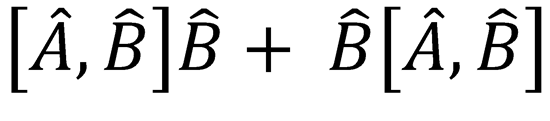2. An H2 or D2 molecule can be idealized as a harmonic oscillator with a force constant k = 575 N m-1. In this
idealization the ground state wavefunctions for H2 and D2 are Gaussians.
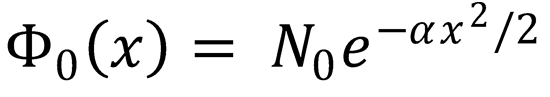
where α = 2πμυ/ħ and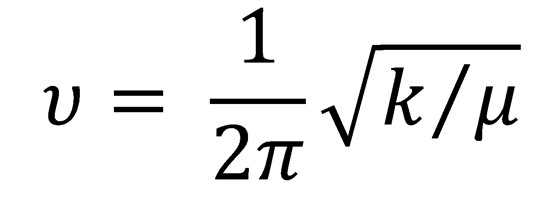 
, with μ the reduced mass
(a) Express the FWHM in terms of μ and k.
(b) What is the FWHM for H2 and D2 in m?
Supposed that the potential holding the atoms together is suddenly "removed" and the molecules travels
through a potential-free region.
(c) Give an expression for the time-dependence of the FWHM.
(d) Calculate the FWHM for both molecules after one vibrational period T = 1/υ.
(e) Calculate the FWHM for both molecules after t = 1 second.
3. (a) Show that
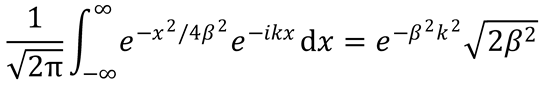
using the standard integral
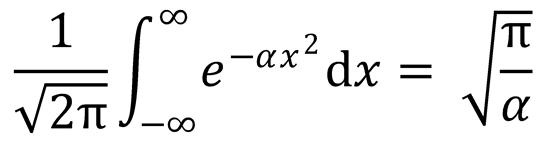
(b) Use the result from (a) to prove Eq. (3.37) from Eq. (3.36).
4. Using Eqs. (B3.5.1)-(B3.5.5) of Study Box 3.5, explicitly derive the elements of the local R-matrix of
Eq. (3.62).
5. Eq. (3.88) gives the relation between ψ(q, t) and ψ(q, t + Δt) via the time evolution propagator.
(a) Give an expression for the relation between ψ(t) and ψ(q, t – Δt) .
(b) Use this relation and Eq. (7.18) to derive an expression for the propagation of ψ(t – Δt) to ψ(t + Δt).
(c) If you use the above result to propagate a wavefunction, do the real part and the imaginary part of the
wavefunction have to be propagated simultaneously or can they be propagated separately? Why?
6. Explicitly derive Eqs. (3.97) (a) and (b).
Above Problems are available as a PDF to print
Solutions to Chapter 3 Problems