1. Imagine a particle confined to an infinitely high walled box, between 0≤x≤a. Assume that it is prepared in a
coherent superposition state described by the time-dependent wavefunction
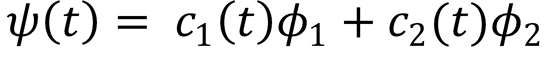
where the coefficients satisfy the equation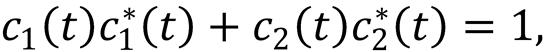 
and the functions 𝜙n, are the particle in a box
eigenfunctions
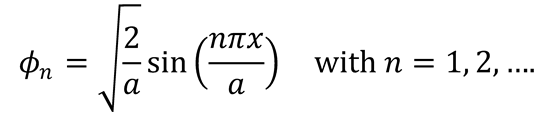
(a) Use the time-dependent Schrödinger equation (see Eq. (3.11)) to show that
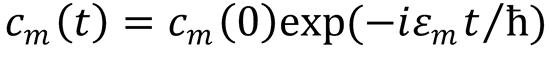
where εm is the eigenstate of , with m = 1 or 2. cm(0) refers to the value coefficent cm(t) at t = 0.
(b) Obtain an expression for ψ(t)ψ*(t) in terms of 𝜙1 and 𝜙2.
(c) Compare the temporal behaviour of ψ(t)ψ*(t) when c1(0) = 1, c2(0) = 0 and c1(0) = c2(0) = 1/√2.
Comment on the answers that you obtain.
[Hint: Based on the expression you obtained in part (b), work out ψ(t)ψ*(t) in terms of 𝜙1 and 𝜙2 at t = 0
and t = π/ω, where ω = (ε2 – ε1)/ħ.]
2. (a) For a pulse with a Gaussian distribution of modes (FWHM 100 nm, centred at 800 nm) and Gaussian
temporal intensity distribution, what is the minimum FWHM pulse duration that can be achieved?
(b) For a pulse of intensity I= 1014 W cm-2, calculate the refractive index of Ti:sapphire at 800 nm. Determine
the phase delay at 800 nm after travelling through:
i. 5 mm of Ti:sapphire (n0 = 1.76, n2 = 3.1 x 10-16 cm2 W-1);
ii. 5 mm BK7 glass (n0 = 1.51, n2 = 3.5 x 10-16 cm2 W-1).
3. Show that the autocorrelation function is given by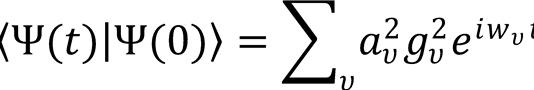 
. Plot the modulus fo the
autocorrelation function following excitation of a wavepacket created from vibrational states centred around
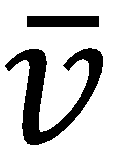= 21, with a transform-limited Gaussian laser pulse fo 40 fs duration, for
(a) a harmonic oscillatior with ωe = 170 cm-1;
(b) an anharmonic oscillator with ωe = 170 cm-1 and ωexe = 2 cm-1.
For a Gaussian pulse,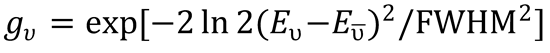 
. For simplicity, assume that av2 is approximately
contstant.
Above Problems are available as a PDF to print
Solutions to Chapter 11 Problems