The following solutions are fully worked through in a PDF that is available to print.
1. Derivation of Eqn (4.5).
Use the Hamiltonian expression: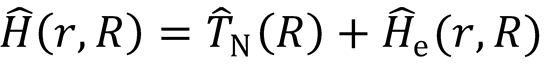 
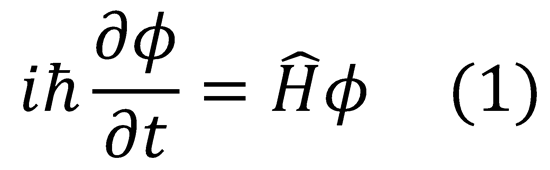
The electronic wavefunctions satisfy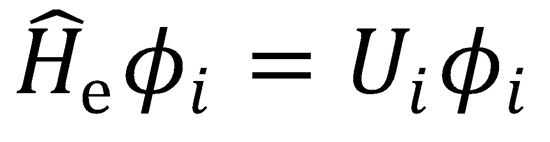 
, where Ui is the electronic energy of the i th state.
N.B. Solutions differ at each set of nuclear coordinates.
Now expand the total wavefunction as the product of the electronic wavefunctions,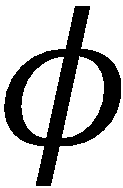 
i, and the
nuclear wavefunctions, ψi.
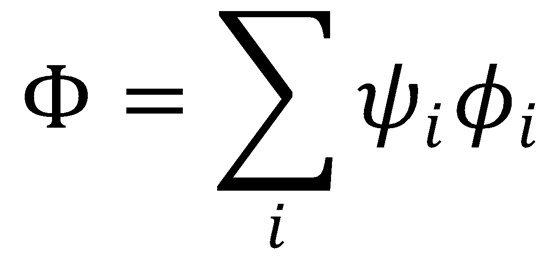
Substitute this back into the full Schrödinger expression (1):
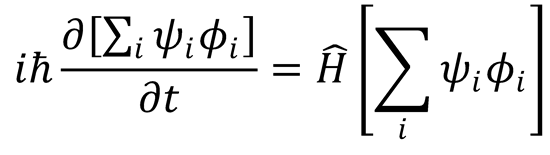
Multiply by 
such that 
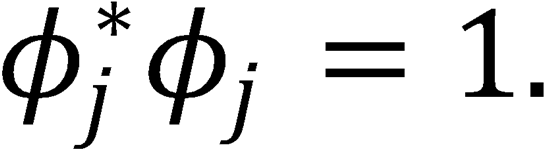
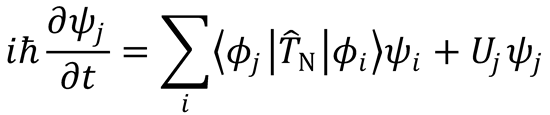
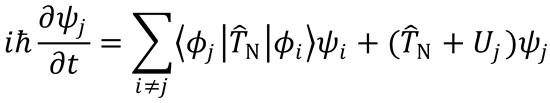
Define (as in Eqn (4.6))
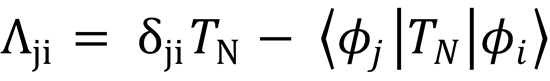
and substitute into the previous equation to obtain Eqn (4.5):
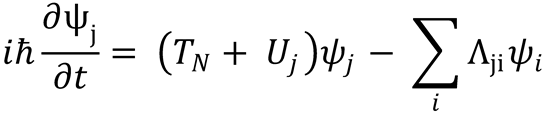
2. Derivation of eqn (4.9). This particular question examines in more details the expressions containing Λij noting
that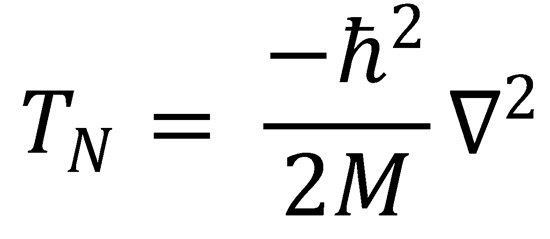 
.
Substitution of this expression for TN into eqn (4.6) gives:
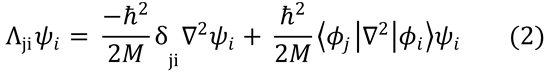
Applying the relationship for the second derivative of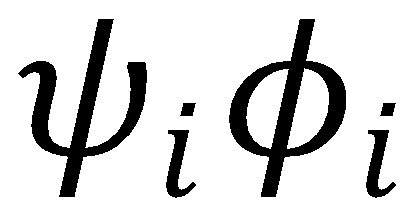 
given in the hint,
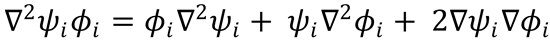
Substitute this into equation (2):
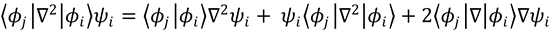
and for j≠i, because of the orthonormality condition for the electronic wavefunctions,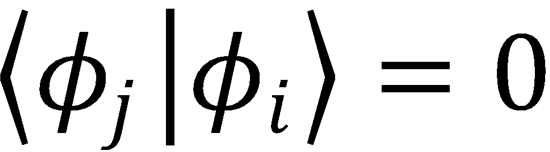 
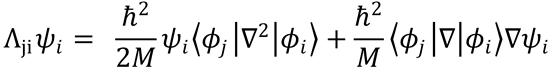
We can therefore write
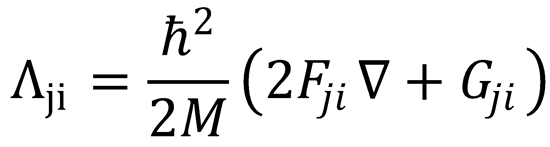
which is eqn (4.8), with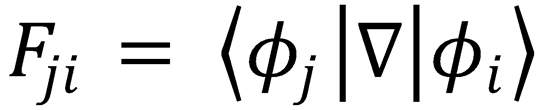 
and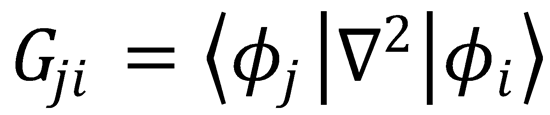 
.
The expression for Fji can be re-written by applying the gradient operator to both sides of the Schrödinger
equation :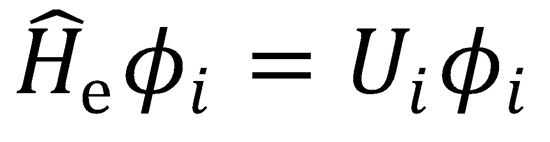
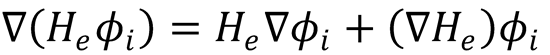
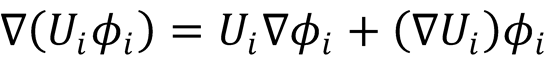
Setting the right hand sides of both equations to be equal, multiplying through by and integrating over
electronic coordinates gives:
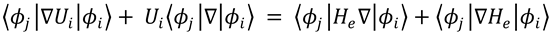(3)
Each term can be evaluated as follows:
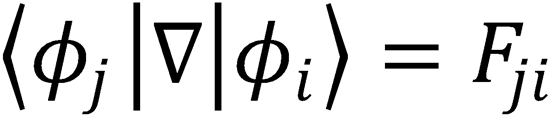from the definition of Fij
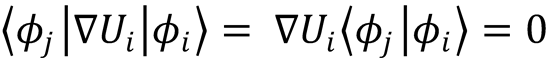for i≠j
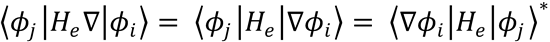
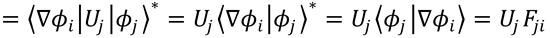
Here, use has been made of the Hermicity of He and the Schrödinger equation .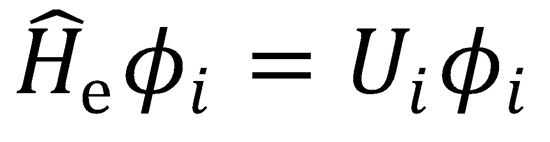
Equation (3) therefore becomes:
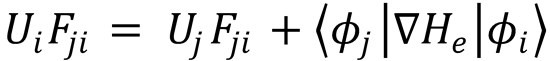
This can be straightforwardly rearranged to
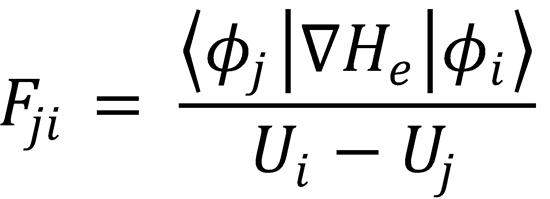
which is eqn (4.9) (QED).
3. This is an example of a harpoon mechanism.
Cs + Br2 → CsBr + Br
Electron transfer occurs at Rc, where:
Vionic(Rc) = Vcovalent(Rc)
Using the equation
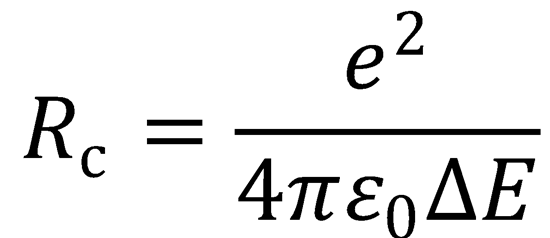
Rc = 10.75 Å
∴ σ = 361.9 Å2
4. Use the variation principle:
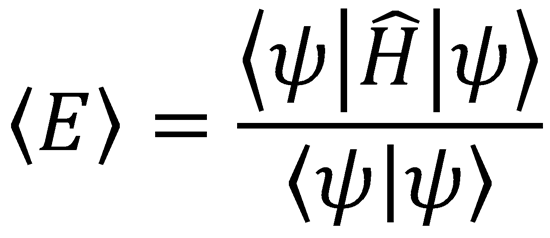
Solve the secular equation
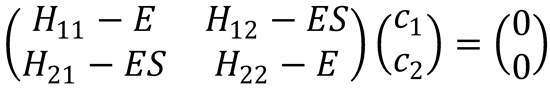
by setting its determinant equal to zero.
The answer you should obtain for the two lowest energy levels is:
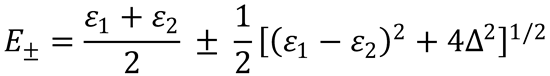(4)
5. Substitute the values given into expression (4) to give (after rearrangement):
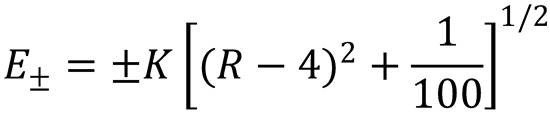
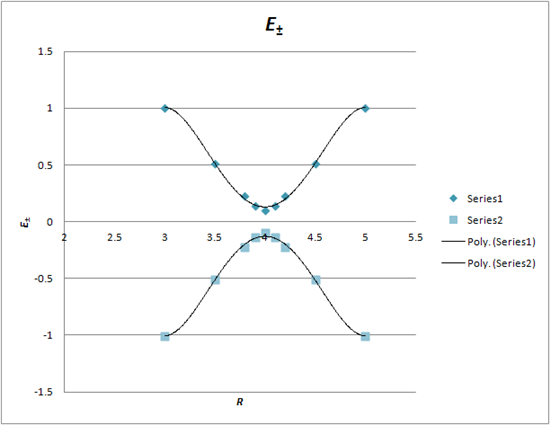
Using this equation, evaluate the two lowest energy levels for the required values of R to give:
|
R |
E± |
|
5.0 |
± 1.005K |
|
4.5 |
± 0.510K |
|
4.2 |
± 0.224K |
|
4.1 |
± 0.141K |
|
4.0 |
± 0.1K |
|
3.9 |
± 0.141K |
|
3.8 |
± 0.224K |
|
3.5 |
± 0.510K |
|
3.0 |
± 1.005K |
Plot these data points to yield a graph that looks like this:
Next, determine the ratio of |c1/c2| as a function of R for each associated eigenfunction. This ultimately
yields the expression:
after substitution of the values for H11, H22, and H12, E± and ε1 into the secular equation (see the PDF for
fully worked solutions).
Then, substitute the values E± and ε1 for the expressions provided in the question to obtain:
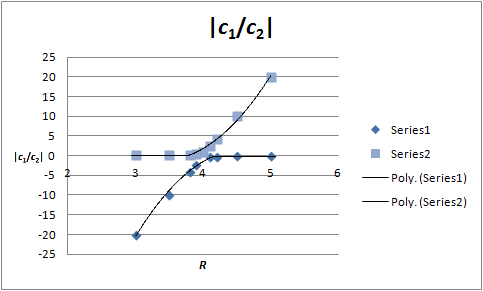
Use this equation to evaluate |c1/c2| as a function of R to produce the following table:
|
R |
|c1/c2| |
|
5.0 |
-0.0499, +20.0499 |
|
4.5 |
-0.0990, +10.0990 |
|
4.2 |
-0.2361, +4.2361 |
|
4.1 |
-0.4142, +2.4142 |
|
4.0 |
± 1.000 |
|
3.9 |
-2.4142, +0.4142 |
|
3.8 |
-4.2361, +0.2361 |
|
3.5 |
-10.0990, +0.0990 |
|
3.0 |
-20.0499, +0.0499 |
Plot these data points to yield a graph that looks like this:
6. The kinetic energy of the I and Br atoms at the crossing between the B and Y potentials is calculated from
the difference between the photon energy and the potential energy:
KE = hν – hcE
with the factor of hc to convert E from units of cm-1 to J.
The reduced mass of IBr is: µ = 49.029 u = 8.144 x 10-26 kg
The relative speed of the I and Br atoms at the crossing point of the two potential energy curves is:
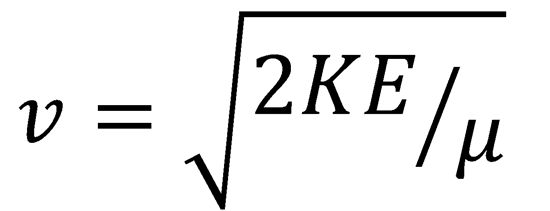
These values and the parameters from the table given can be inserted into eqn (4.4).
For example, for a photon with energy = 19000 cm-1, ν = 992 m s-1 and P = 0.765 is the probability of
nonadiabatic dynamics (i.e. remaining on the diabatic B-state potential).
Thus, the probability of crossing from the diabatic B state to the Y state is PB/Y = 1 – P = 0.235.
The other values plotted in figure 4.4 can be derived in a similar way.
N.B. the unit of Å-1 must be converted to m-1 as part of the calculation.
7. For the collinear reaction of F(2P3/2) + H2 the total electronic angular momentum quantum number is J = 3/2
(the H2 in its electronic ground state has no electronic angular momentum).
Allowed values of Ω correspond to the projections of J on the internuclear axis, and are Ω = 3/2, 1/2.
For the HF(X1Σ+) + H(2S1/2) products, J' = 1/2, with the ' denoting product quantum numbers.
For HF (a3Π) + H(2S1/2) products, Ω'HF = 0, 1 and 2, and Ω'H = 1/2, giving possible values of Ω' = 1/2, 3/2
and 5/2.
The adiabatic correlations are thus:
F(2P3/2) + H2 (Ω = 1/2) → HF(X1 +) + H(2S1/2) (Ω' = 1/2)
F(2P3/2) + H2 (Ω = 3/2) → HF(a3Π) + H(2S1/2) (Ω' = 3/2)
F(2P1/2) + H2 (Ω = 1/2) → HF(a3Π) + H(2S1/2) (Ω' = 1/2)
in accord with figure 4.11.
Similar arguments give the correlations shown in figure 4.11 for the F + D2O → DF + OD reaction (treating the
reaction as collinear), with the additional complication that the ground electronic state of OD is a 2Π state with
Ω'OD = 3/2 and 1/2.
Return to Problem Set