The following solutions are fully worked through in a PDF that is available to print.
1. This is described using the Langevin model.
The classical motion of two structureless atoms is fully characterised by the Hamiltonian equation of motion:
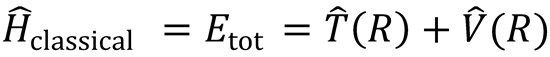
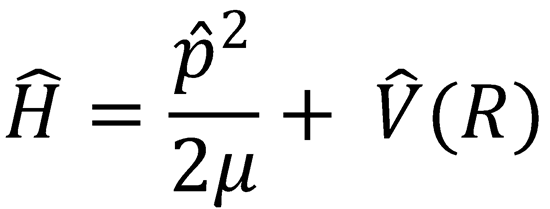
This represents the total energy associated with the relative motion of the system, which is conserved during
the collision.
When the particles are at infinite separation, the potential energy ≈ 0, and so the Hamiltonian may simply be
written as the initial relative kinetic energy of the particles, Et.
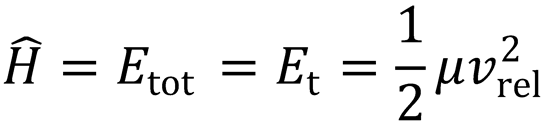
Written in polar coordinates:
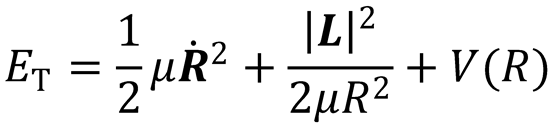
The first term in this expression is the kinetic energy associated with the relative motion of the two atoms
toward each other; it is the radial kinetic energy. The second term is the centrifugal kinetic energy, and is
the energy associated with the orbital motion of the particles with orbital angular momentum, L. Both the
direction and magnitude of the orbital angular momentum are conserved during an elastic collision between
atoms.
i.e.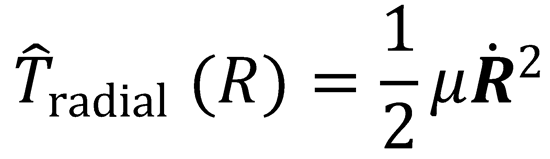 
(where 
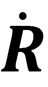is the rate of change of separation of two particles), and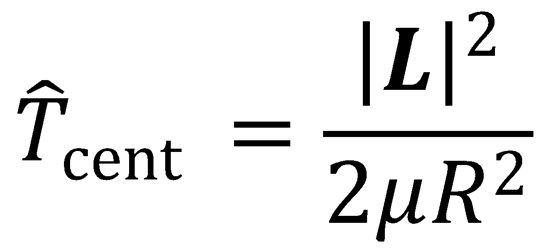 
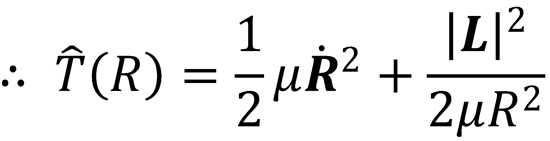
We can also write:
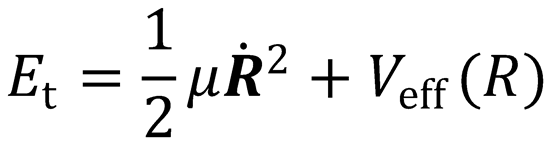
where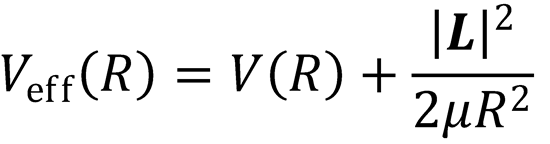 
i.e. Veff(R) is the potential energy, accounting for the centrifugal barrier term.
N.B. the kinetic energy associated with orbital motion is not available to help surmount an activation barrier,
and so it has the effect of reducing the available energy. This centrifugal barrier can given rise to an
effective barrier to the reaction, even when the PES itself has no barrier.
|L| = μvrelb
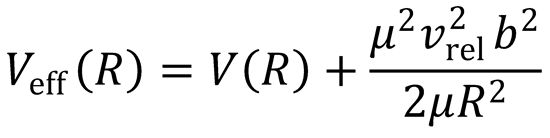
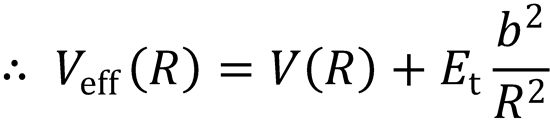
where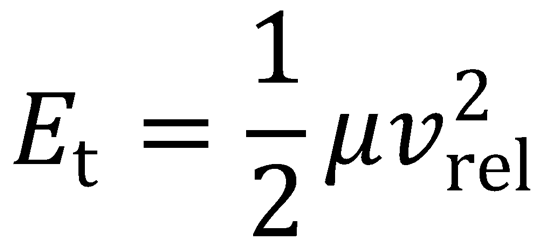 
(b)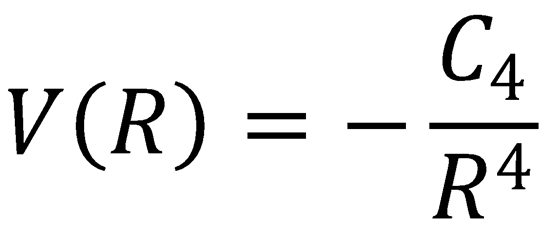 
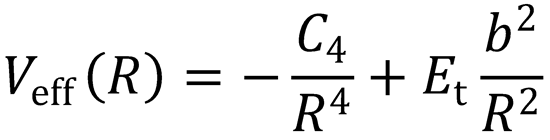
There is a maximum in the centrifugal barrier at R = R0. This occurs when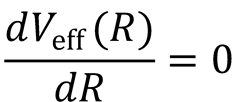 
:
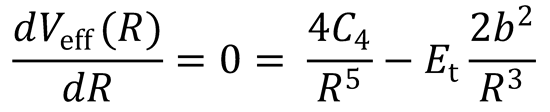
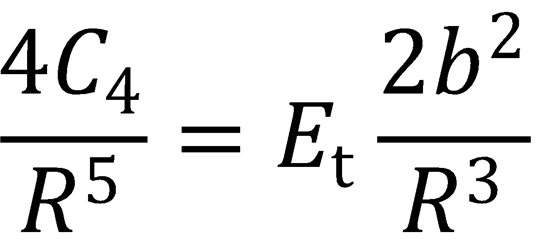
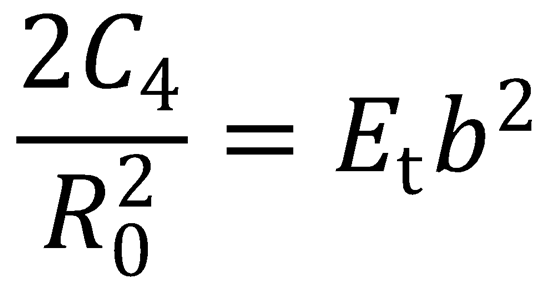
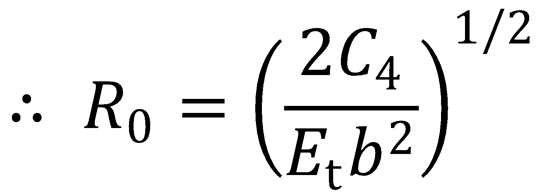(QED)
(c) At the centrifugal barrier, the radial kinetic energy,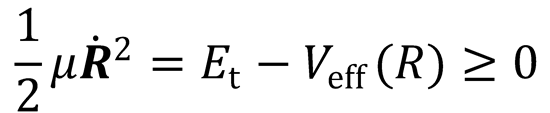 
, at R0.
Substitute for R0 in the expression for Veff(R):
The capture cross section is determined using the expression:
where the opacity function, P(b), is assumed to be equal to unity.
Integrating this expression yields:
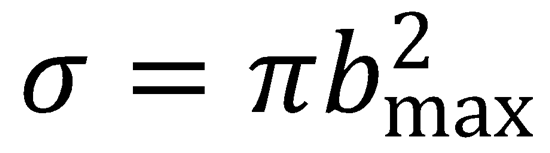
Substituting the expression for bmax determined above:
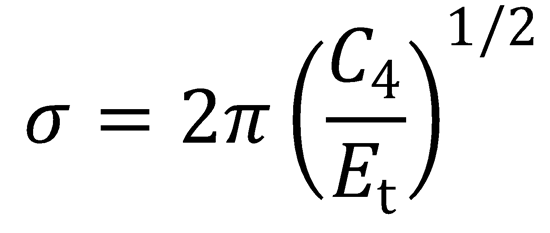
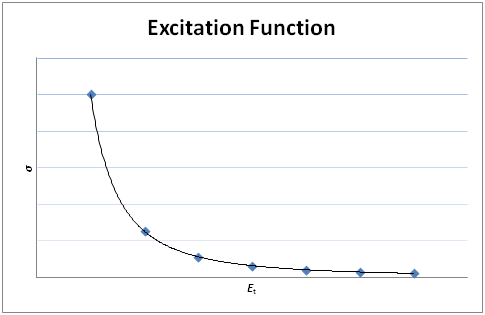
The excitation function shows the dependence of the cross section on the collision energy, Et.
As Et → 0, σ → ∞.
N.B.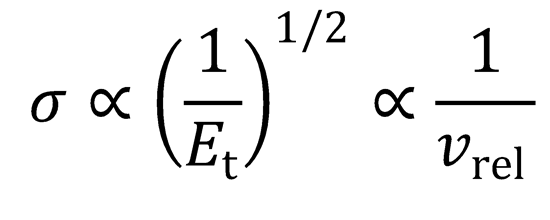 
This has implications for the rate constant at low temperatures.
Sketch of the excitation function:
(e) α'(O2) = 1.4 x 10-30 m3
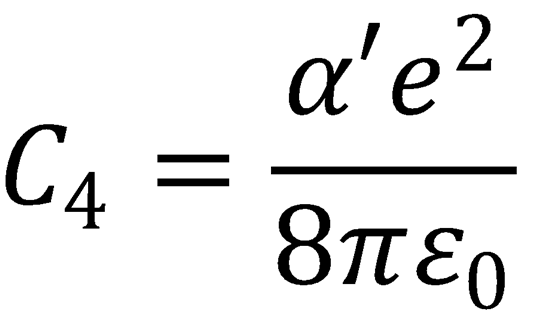
∴ C4 = 1.61 x 10-58 J m4
From the equipartition principle: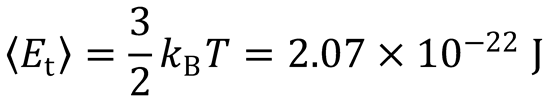 
at 10 K.
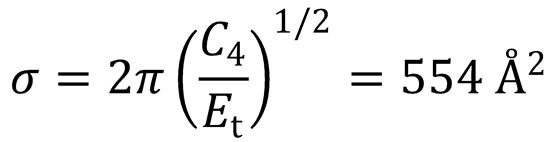
This is a very large ion-induced contribution to the capture cross-section since there is no
barrier to the reaction, and hence a very low Et at low temperatures.
Return to Problem Set