1. (a) Determine the collision frequency of an OH radical in 100 mTorr of Ar. Assume that the collision cross
section is 50 Å2.
(b) Use Poisson statistics to estimate the fraction of OH radicals that have undergone zero, one, or two
collisions at a time delay of 50 ns after their photolytic production (e.g. via the photodissociation of
hydrogen peroxide).
2. The reaction
K + I2 → KI + I
was studied at a mean relative velocity of 800 ms-1, with I2 in thermal equilibrium at 300 K. The reaction
cross section was found to be 170 Å2. Use the data in the table below to estimate
(a) the total energy available to the products,
(b) the maximum orbital angular momentum quantum number, l max, and
(c) the rotational energy of the KI product if j' = l max, where j' is the rotational angular momentum
quantum number for KI.
Identify any assumptions made in obtaining the estimate in (b).
|
|
I2 |
KI |
|
D0/kJ mol-1 |
149 |
319 |
|
ωe/cm-1 |
214.5 |
186.5 |
|
Be/cm-1 |
0.037 |
0.061 |
[The mean vibrational energy of the I2 reactants may be calculated assuming Ev = hcωe/(eθv/T - 1) with
θv = hcωe/kB.]
3. The cross section, σr(Ec), for the endothermic reaction
K + HCl → KCl + H
increases with the collision energy, Ec, in the following way:
|
Ec/kJ mol-1 |
9 |
15 |
30 |
50 |
|
σr(Ec)/10-20m2 |
0.5 |
1.25 |
2.0 |
2.2 |
(a) Show that the cross section data are consistent with the line-of-centres model
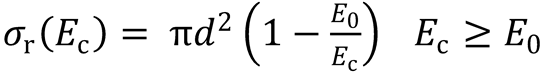
and determine the threshold energy, E0, and the limiting, high collision energy cross section, πd2.
(b) In terms of the reaction cross section, the thermal rate constant can be written
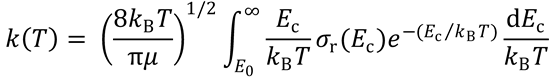
Use this equation to obtain a line-of-centres expression for k(T). Comment on the result you obtain. You
may use the following integral without proof
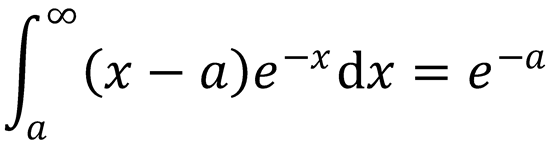
4. Explain how the constraints imposed by the conservation of angular momentum influence the disposal of
rotational energy in the reaction
Ba + HI → BaI(v', j') + H
This reaction has been studied under crossed molecular beam conditions, at a reactant relative velocity
vrel = 976 ms-1; the rotational state distribution in the product, BaI, was found to peak at the value
j' = 420. Given the orbital angular momentum of the reactants in this reaction can be written |l | = μvrelb,
estimate the most probable impact parameter, b, and the reaction cross section.
[Take the masses to be mBa = 137.3 u, mH = 1.0 u, and mI = 126.9 u.]
Above Problems are available as a PDF to print
Solutions to Chapter 1 Problems