1. The xyz and x'y'z' reference frames of Figure 9.2 are respectively biased towards reactants and products. Can
you think of an unbiased body-fixed reference frame?
2. The vector hierarchy used in Figure 9.3 was k → k' → j, j'. Redraw the figure using a different hierarchy,
k → j → k', j'.
3. Using theoretical methods, the authors of ref. [694] have associated a non-adiabatic effect in the dynamics of
the H + H2 reaction with product scattering into positive or negative "deflection angles", see Figure 5 of that
paper. Experimentally, positive and negative deflection angles cannot be distinguished - they correspond to
the same scattering angle. Reactant or product polarization measurements, however, might allow experimental
observation of the distinct reaction mechanisms. How?
Hint: see Problem 2.
4. When reaction (9.69) proceeds via mechanism a, the real PPs of reactants and products are those on the top
row of Table 9.2. What are the values of their complex PPs?
5. A diatomic molecule is in a j = 1 rotational state. Calculate its density matrix, knowing that its non-vanishing
complex polarization moments are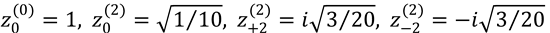 
. Is this molecule polarized? If
so, how?
6. Using the data below, obtain mathematical expressions for the axial and rotational PDFs of the molecule of
Problem 5. From the mathematical expressions, can you tell how the molecule is polarized?
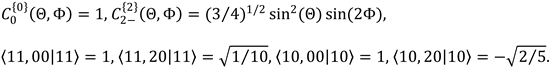
7. In the trajectory of Figure 9.8 the internuclear axes of the reactant and product diatomics are oriented. But
we have seen that, besides being incompatible with the axial portrait of Figure 9.12, this cannot happen.
Show that indeed it does not. Hint: draw a new trajectory using reflection through the scattering plane. Can
the new trajectory be more or less likely than the original?
8. Use Eqs. (9.18) and (9.22) to show that the complex polarization moments of a density matrix satisfy
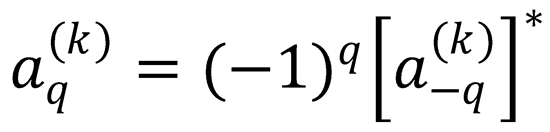
Hint: Use the fact that the density matrix is Hermitian (that is, 
), and the formula239,647
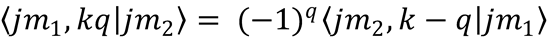
9. Chemical reactions conserve parity. This implies645 that the elements of helicity-representation scattering
matrices satisfy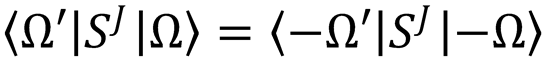 
, which in turn implies that the density matrix of Eq. (9.36) satisfies
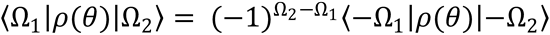
Use this property to show that the polarization moments of ρ(θ) satisfy
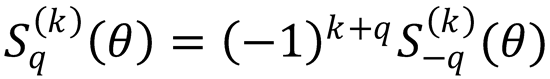
Hint: Use Eq. (9.18) and the formula239,647
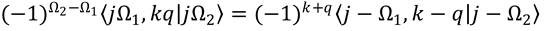
10. Combining the results of Problems 8 and 9, and noting that the symmetry properties obtained there are
independent of whether the polarization moments are normalized PDDCSs, renormalized PDDCSs or PPs,
we find that the intrinsic polarization moments of chemical reactions must satisfy
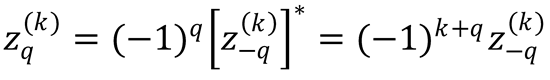
where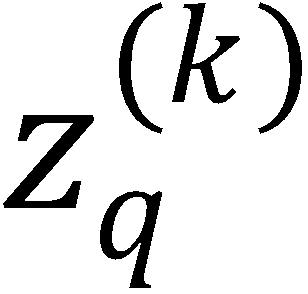 
stands for any of those polarization moments. Use these equalities to prove the following:
(a) If k is even, then the complex polarization moments are actually real.
(b) If k is even, then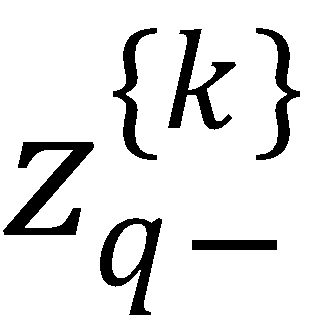 
polarization moments vanish.
(c) If k is odd, then the complex polarization moments are actually pure imaginary.
(d) If k is odd, then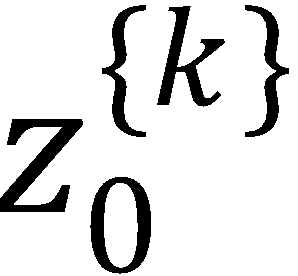 
and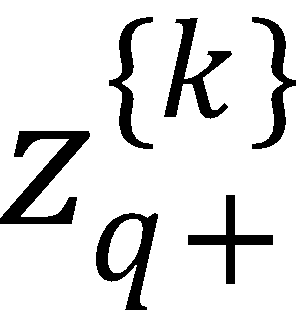 
polarization moments vanish.
11. Conservation of parity also implies that the intrinsic rotational PDFs of chemical reactions must satisfyy
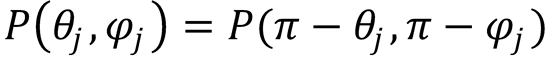
Using this symmetry property and Eq. (9.32) - the classical expansion of rotational PDFs - show that the
classical normalized PDDCSs satisfy
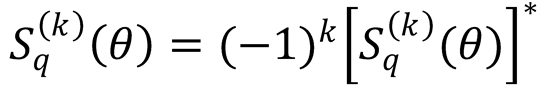
and therefore that they also follow the rules specified in items (a-d) of Problem 10. Hint: Use the following
formula:647
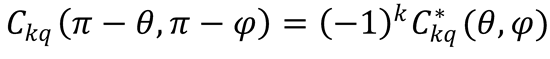
12. Using the space-fixed frame described in Section 9.3.1.1, sketch an approach geometry one might observe
at the start of a classical trajectory. How do the positions of the atoms depend on the collision parameters?
13. Show that the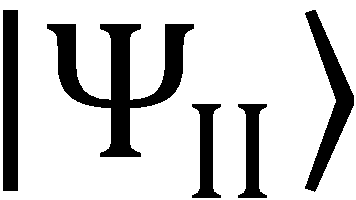 
state of Eq. (9.81) is such that 
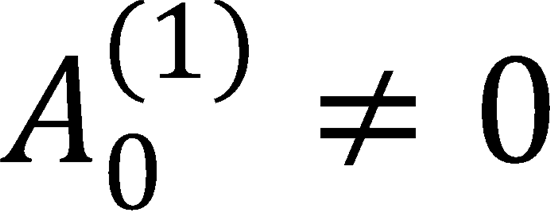. Taking into consideration the conditions for
intrinsic PP values determined in Problem 10, decide how the non-vanishing extrinsic A0{1} will affect the
reaction stereodynamics.
14. Prove the second equality of Eq. (9.78). Hint: First, rewrite Eq. (9.79) using, for each mechanism,
dσ/dω = (σ/2π)P(θ). Next, expand Tr(ρiρe) using Eq. (9.21) twice; note that the expansion coefficients of
Pa(θ)ρa are the normalized PDDCSs of mechanism a, and similarly for mechanisms b and c. Finally, use this
formula:647
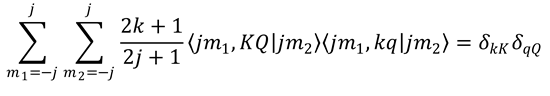
15. Derive Eq. (9.84) from Eq. (9.78). Hint: Integration over θ transforms the complex normalized PDDCSs into
complex PPs, see Eq. (9.25); integration over φ averages the PPs with q ≠ 0 to zero; the remaining PPs have
q = 0 and are therefore real, see Eq. (9.11c).
16. This problem involves fairly long calculations requiring the values of CG coefficients and rotation matrix
elements; the supplementary material contains a Maple® worksheet enabling automatic performance of all
calculations. As the states and conditions involved can be changed by the user, this problem could be used
for a class tutorial, with each student doing different but entirely analogous calculations.
As discussed in Chapter 12, an ultracold reaction proceeds only via the partial wave associated with ℓ = 0.
A consequence of this is that the scattering matrix elements are independent of reactant helicity.696 As
the S elements also satisfy 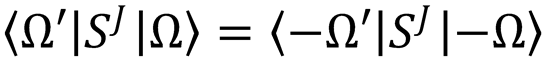(see Problem 9), for small j and j' values there are few
S elements one needs to consider, and fewer still whose calues can be independently varied. The problem
consists in choosing arbitrary values for the problem parameters and then analyzing the resulting
stereodynamics.
(a) Specify the values of j and j'. (The data in the worksheet allows for calculations involving j ≤ 5 and
j' ≤ 5.)
(b) Noting that the ℓ = 0 condition implies j = J, decide what S elements can be independently varied, and
then assign an arbitrary complex value to each of them. (The worksheet will check whether your
specification allows for a full, unique specification of the required S elements, and then scale them so that
σur = 10 Å2.)
(c) Choose a reference frame for the stereodynamical analysis.
(d) Follow the instructions in the worksheet to calculate the following:
i. DCS of the reaction involving unpolarized reactants, dσur/dω.
ii. Intrinsic density matrices of reactants and products.
iii. Intrinsic real renormalized PDDCS of reactants and products and the associated stereodynamical
portraits.
iv. Intrinsic real PPs of reactants and products and the associated portraits.
(e) From this data, rationalize the stereodynamics and comment on the possibilities of ICS and DCS control
via reactant polarizaton. Hint: Think about the consequences of the ℓ = 0 restriction for the approach
direction from the viewpoint of reactive collisions, and also about the consequences of j = J and total
angular momentum conservation.
(f) Specify a set of directions for r alignment, and then use the worksheet to calculate the resulting ICSs
and DCSs. Are the results consistent with your answer to item (e)?
(g) Use the worksheet to disentangle the independent reaction mechanisms and calculate the
stereodynamical properties of each of them.
(h) Rationalize the stereodynamics of the various independent mechanisms. Hint: Rather than thinking
about the mechanisms in terms of classical trajectories, think about angular momentum conservation.
Above Problems are available as a PDF to print
Solutions to Chapter 9 Problems