Chapter 2 - Tutorials in Molecular Reaction Dynamics

1. (To answer this question fully requires knowledge of some of the material covered in Chapters 1, and

Chapters 5 to 7, including Study Box 7.1.)

(a) Briefly outline experimental strategies currently available for measuring the partitioning of energy

between vibration, rotation, and translation in the products of an exothermic atom transfer reaction

A + BC → AB (v', j') + C

(b) How may the properties for vibrational and translational energy disposal be influenced by the topography

of the potential energy surface over which the reaction proceeds, and by the masses of the atoms

involved? Illustrate your answer by reference to the data, determined at 300 K, for the following reactions

[〈f_vib〉 and 〈f_trans〉 are the mean fractions of the total energy disposed into vibration and translation,

respectively.]

2. In this question we use a very simple theory of bonding, known as Hückel theory, which ignores the effects

of electron repulsion and electron correlation, to obtain information about the relative barrier heights of two

reactions.

Use Hückel theory and the variation principle to construct the secular equations for the π orbitals of the allyl

radical shown below.

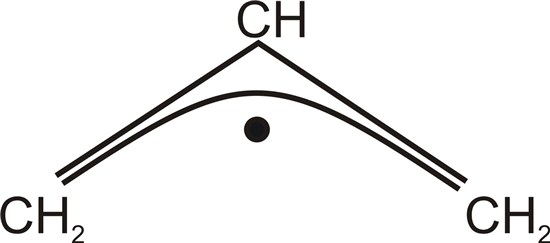
Determine the molecular orbital energies and the linear combinations of atomic orbitals associated with

them. Show that the charge density arising from the π electrons is uniform at each carbon atom in the allyl

radical. Using Hückel theory to estimate the appropriate barrier heights, suggest the most likely point of

attack on the allyl cation, C₃H₃⁺, by a nucleophilic reactant. You many assume that the σ-bonding

framework is unaffected by the attack of the nucleophile.

3. (a) How is a stationary point on a PES defined? What differentiates a saddle point from an energy minimum?

(b) What information do we commonly calculate from the Hessian of the PES (a generalization of the second

derivative of the energy for a diatomic molecule) at an energy minimum? Can you relate this information

to Newton's law for motion close to the energy minimum? What corresponding information could we

calculate from the Hessian at a saddle point?

many chemical reactions, there are many stationary points on a PES (e.g. Figure 2.4). Quantum chemistry

programs can determine stationary points on a PES. Given that a saddle point geometry has been found,

how would you determine which 'reactants' and 'products' are connected by this saddle point?

Potential Energy Surfaces: the Forces of Chemistry