The following solutions are fully worked through in a PDF that is available to print.
2. (a) Using the fact that for a pulse with a Gaussian distribution of modes and Gaussian temporal intensity
distribution, the time bandwidth product is 0.441 (Eq. (11.1))
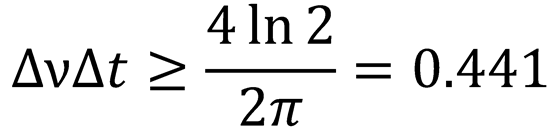
Δν = 100 nm centred at 800 nm
= 4.7 x 1013 Hz
∴ Δt = 0.441/4.7 x 1013
= 9.38 fs
(b) i. This part exploits the optical Kerr effect.
Using the expression n = n0 + n2I we obtain:
n = 1.76 + (3.1 x 10-16 x 1014)
= 1.791
The phase delay is given by:
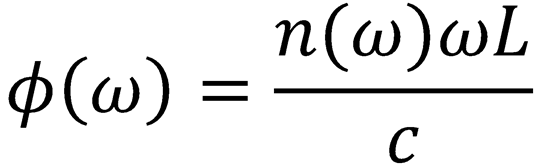(Eq. (11.2))
Since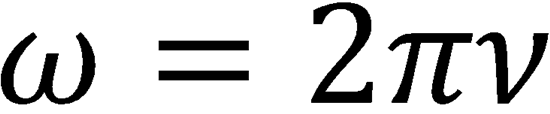 
, this can be rearranged to give:
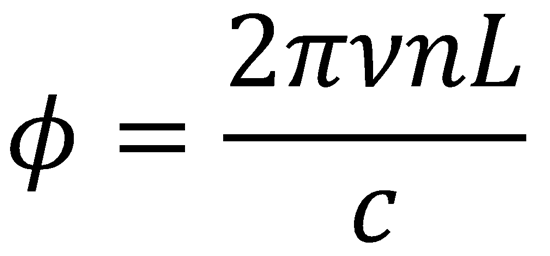
𝜈 = c/𝜆
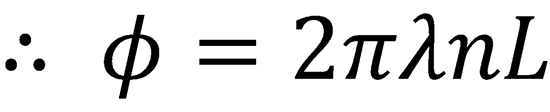
λ = 800 x 10-9 m, L = 0.005 m
= 4.5 x 10-8
ii. Using the expression n = n0 + n2I we obtain:
n = 1.545
Now, using the equation:
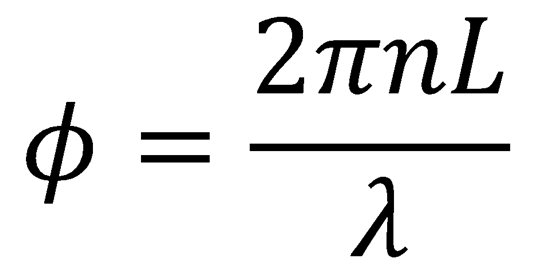
= 6.07 x 104
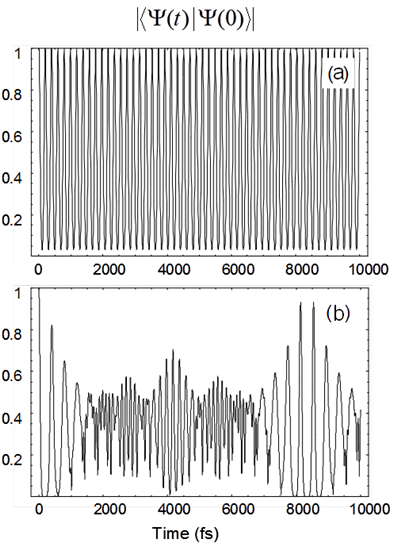
3. The large spectral width of a femtosecond light pulse results in a number of molecular eigenstates being
excited coherently, and this coherent superposition of wavefunctions then evolves over time.
An example of a coherent oscillation is one that results from a coherent superposition of vibrational
wavefunctions, . The resulting wavepacket is written as:
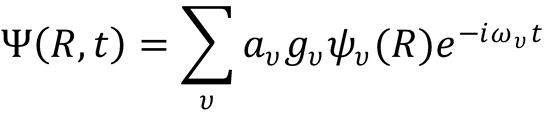
from Eq. (11.10).
The wavepacket oscillates back and forth along the internuclear coordinate at the vibrational period.
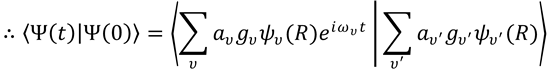
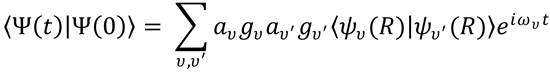
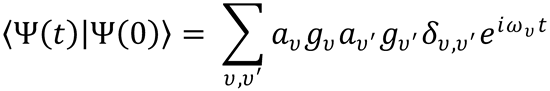
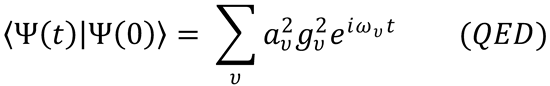
(a) Plot for a harmonic oscillator with 𝜔e = 170 cm-1.
(b) Plot for an anharmonic oscillator with 𝜔e = 170 cm-1 and 𝜔exe = 2 cm-1.
These plots are shown below.
Return to Problem Set